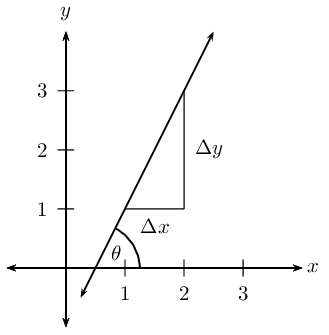
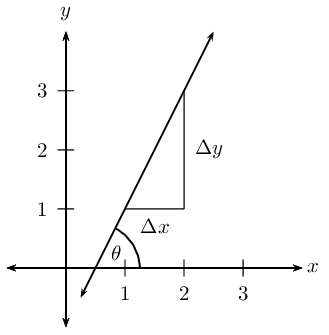
The diagram shows that a straight line makes an angle \(\theta\) with the positive \(x\)-axis. This is called the angle of inclination of a straight line.
We notice that if the gradient changes, then the value of \(\theta\) also changes, therefore the angle of inclination of a line is related to its gradient. We know that gradient is the ratio of a change in the \(y\)-direction to a change in the \(x\)-direction:
From trigonometry we know that the tangent function is defined as the ratio:
And from the diagram we see that
\begin \tan \theta &= \dfrac \\ \therefore m &= \tan \theta \qquad \text < for >\text\text \leq \theta < \text\text \end
Therefore the gradient of a straight line is equal to the tangent of the angle formed between the line and the positive direction of the \(x\)-axis.
Vertical lines
Horizontal lines
Lines with negative gradients
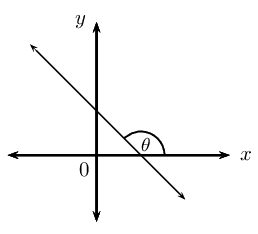
From the CAST diagram in trigonometry, we know that the tangent function is negative in the second and fourth quadrant. If we are calculating the angle of inclination for a line with a negative gradient, we must add \(\text\text\) to change the negative angle in the fourth quadrant to an obtuse angle in the second quadrant:
If we are given a straight line with gradient \(m = -\text\), then we can determine the angle of inclination using a calculator:
\begin \tan \theta &= m \\ &= -\text \\ \therefore \theta &= \tan^(-\text) \\ &= -\text\text \end
This negative angle lies in the fourth quadrant. We must add \(\text\)\(\text\) to get an obtuse angle in the second quadrant:
And we can always use our calculator to check that the obtuse angle \(\theta = \text\text\) gives a gradient of \(m = -\text\).
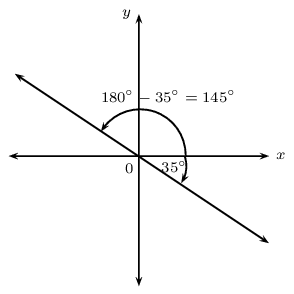
Determine the gradient (correct to \(\text\) decimal place) of each of the following straight lines, given that the angle of inclination is equal to: